Farben haben den Menschen seit Urzeiten begleitet. Jeden Tag können wir ihre Schönheit und Vielfalt neu erfahren, denn sie sind für uns immer noch ein Rätsel. In unseren früheren Artikeln haben wir uns damit befasst, was Farben sind und welche Farbmodelle es je nach Gerät gibt. Diesmal möchten wir Ihnen ein paar weitere Modelle vorstellen, die bereits zu Beginn des 20. Jahrhunderts gefragt waren.

Im Jahr 1931 wurde im Auftrag der „Commission Internationale de l’Eclairage“ (Internationale Beleuchtungskommission) ein geräteunabhängiges Farbmodell entwickelt. Es wurde auf der Grundlage von Untersuchungen an einer Gruppe von etwa zwanzig Personen erstellt, die in der Lage waren, Farben richtig zu unterscheiden. Dieser Gruppe wurden in einem sehr engen Blickfeld (2°) verschiedene Farben gezeigt, und sie hatten die Aufgabe, diese zu unterscheiden. Die statistische Analyse der Antworten ermöglichte die Entwicklung eines Standardbeobachtermodells. Es zeigt die gemittelten menschlichen Fähigkeiten in Bezug auf die Farbwahrnehmung (z.B. Wellenlängenbereich, Empfindlichkeit, etc.). Auf der Grundlage des Standardbeobachtermodells wurde das CIE XYZ-Modell entwickelt, d.h. das erste geräteunabhängige Farbmodell.
Die CIE XYZ-Methode wird als ein Farbraum bezeichnet, der als Referenz und Standard für andere Farbräume, die von der Commission Internationale de l’Eclairage geschaffen wurden, gilt (CIE LUV, CIE Labor).
Das Konzept der drei Farbwerte von XYZ basiert auf der Idee des Farbensehens, die besagt, dass das Auge aus drei Arten von Photorezeptoren besteht, die es ermöglichen, die drei Grundfarben (rot, grün, blau) zu sehen, während alle Farben Mischungen der drei Grundfarben sind. Daher wird die Farbe in den Trichromatischen Koordinaten X, Y, Z beschrieben. Diese Koordinaten entsprechen den einzelnen Prozentsätzen der drei Grundfarben R (red – rot), G (green – grün) und B (blue – blau).
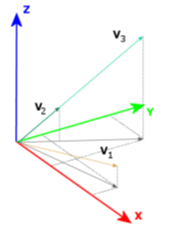
Abb. 1 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
Die dreidimensionale Beschreibung von CIE XYZ wurde in den zweidimensionalen Raum CIE xyY transformiert. Sie wandelt die Farbkomponenten X, Y, Z in die dreifarbigen Koordinaten x, y, Y um. Dabei bestimmen die x- und y-Koordinaten die Farbigkeit und Y die Helligkeit. Der xyY-Raum wird im Farbraum, welcher die Farbtafel ist, als Maxwell-Dreieck oder Farbdreieck dargestellt. Dies wird als eine von zwei Linien eingeschlossene Fläche dargestellt – eine monochromatische Farbkurve und eine gerade violette Linie.
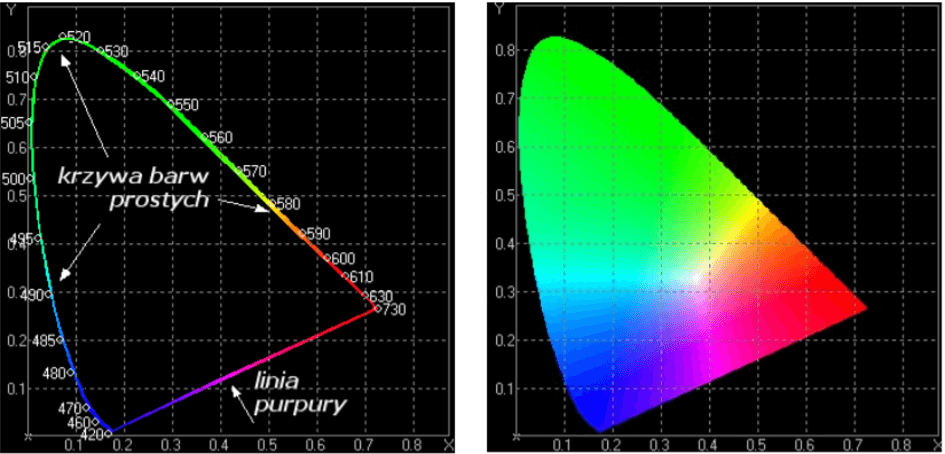
Abb. 2 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
Als Ergebnis der von Wright, MacAdam und Stiles durchgeführten Arbeiten zur Frage der Wahrnehmung von Farbunterschieden wurde die Frage nach der Einheitlichkeit des Farbraums gestellt.
Wenn der CIE XYZ-Farbraum die Bereiche der Farbwahrnehmungsdifferenz bestimmt (Abb. unten), dann erscheinen Ellipsoide unterschiedlicher Größe (sogenannte MacAdam-Ellipsoide). Sie erscheinen in grünen Bereichen, als Ellipsoide mit einem relativ großen Durchmesser und in blauen Bereichen, hier jedoch mit einem relativ kleinen Durchmesser. Wenn wir also zwei Punkte in einem solchen Raum kennzeichnen, kann das menschliche Auge sie als zwei subjektiv unterschiedliche Farbtöne wahrnehmen. Andererseits können zwei gleich weit entfernte Punkte im Grünbereich die Farbtöne bestimmen, zwischen denen das menschliche Auge den Unterschied nicht wahrnimmt, d.h. es handelt sich um einen subjektiv bestimmten Einzelfarbton.
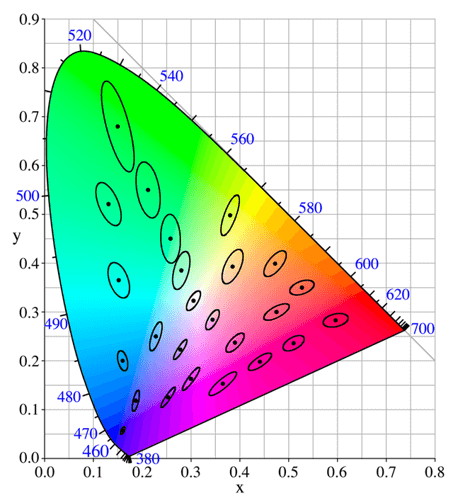
Abb. 3 https://stackoverflow.com/questions/25184748/represent-cie-1931-color-space
Dank der Untersuchungen über die Einheitlichkeit des Farbraums wurden auch die Farbräume CIE LUV und CIE Lab geschaffen.
Das CIE-LUV-Modell wurde (1960) als Ergebnis der Transformation von xy-Variablen in uv-Variablen erstellt. Sie sollten die Unterschiede zwischen den Farben besser wiedergeben. Bei weiteren Untersuchungen stellte sich jedoch heraus, dass ein solcher Satz von Variablen die Bereiche um Braun, Orange und Gelb stark einschränkt. Da die genannten Farbtöne in der Malerei, insbesondere in der Öl- oder Naturmalerei, sehr wichtig sind, mussten weitere Transformationsversuche unternommen werden. 1976 wurden die Variablen u‘ und v‘ entwickelt, wodurch der Raum CIE LU’V‘ entstand. Es ist wichtig, dass sich der Buchstabe „L“ in den Namen hier vom Wort „Lightness“ herleitet und genau wie das „Y“ im xyYY-Modell die Helligkeit definiert. Die beiden erhaltenen Farbräume sind in der folgenden Abbildung dargestellt:
a) CIE uv-Diagramm b) CIE u’v‘-Diagramm
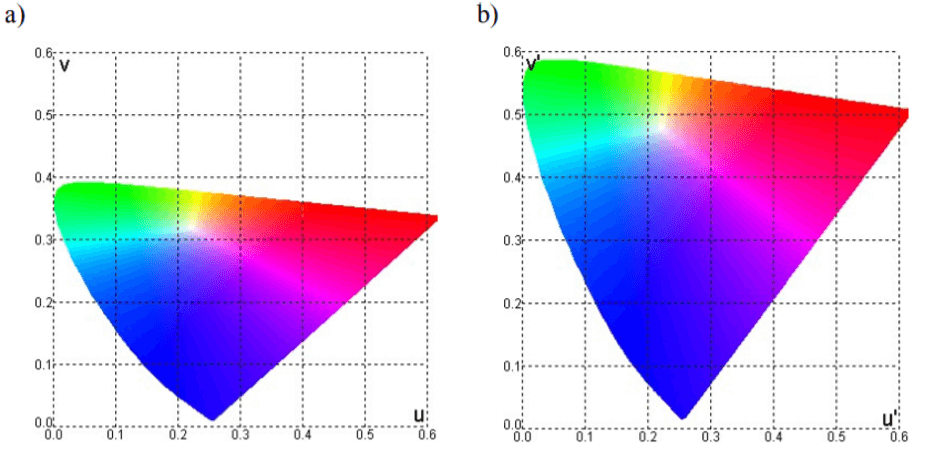
Abb. 4 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
Das zweithäufigste geräteunabhängige Farbmodell ist das Modell CIE Lab. Dies ist eine weitere Umgestaltung des CIE XYZ-Raums, der 1976 geschaffen wurde. Bei der Definition wurde davon ausgegangen, dass Farben, die im gleichen Abstand zueinanderstehen, als gleich unterschiedlich wahrgenommen werden. Unter der Annahme, dass die Farbe nicht gleichzeitig violett, blau und gelb oder grün sein kann, wurden die folgenden Komponenten zur Beschreibung gewählt: L – Helligkeit (Lumination), a – Grün bis Magenta und b – Blau bis Gelb.
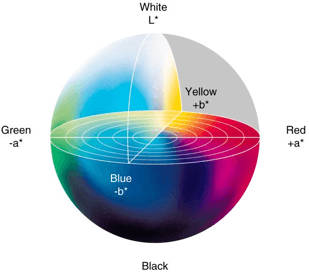
Abb. 5 https://www.researchgate.net/figure/CIE-LAB-1976-color-space_fig2_263697963
Ein wichtiger Vorteil eines bestimmten Modells ist jedoch der einfache Farbvergleich. Der Unterschied zwischen beiden Farben im Raum CIE Lab wird als ΔE ausgedrückt, was sich aus der folgenden Gleichung errechnet:
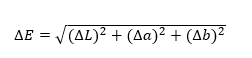
ΔE ist der normale euklidische Abstand zwischen zwei Punkten im dreidimensionalen Raum.
Es wird davon ausgegangen, dass ein Standardbeobachter den Farbunterschied anhand der folgenden Indikatoren erkennt:
0 < ΔE < 1 – sieht keinen Unterschied,
1 < ΔE < 2 – nur ein erfahrener Beobachter erkennt den Unterschied,
2 < ΔE < 3,5 – auch ein unerfahrener Beobachter erkennt den Unterschied,
3,5 < ΔE < 5 – der Betrachter erkennt einen deutlichen Farbunterschied,
5 < ΔE – der Betrachter nimmt die Farben als völlig unterschiedlich wahr.
Wie der CIE XYZ-Farbraum ist auch das Modell CIE Lab mit der direkten Wahrnehmung von Farben durch das menschliche Auge verwandt. Deshalb bezeichnen wir es als geräteunabhängiges Farbmodell.
Der CIE LCh-Farbraum verwendet das gleiche Schema wie der CIE Lab-Farbraum, jedoch mit zylindrischen statt rechteckigen Koordinaten. In diesem Farbraum steht L für die Helligkeit und ist derselbe Parameter wie die Helligkeit L im Raum CIE Lab, C für die Sättigung und h für den Farbton. Der Sättigungswert von C ist im Zentrum der Kugel, die das Abbild des Farbraums darstellt, 0 und nimmt mit dem Abstand vom Zentrum zu. Der Farbton h ist der Winkel, dessen Messung an der + a-Achse beginnt und in Grad ausgedrückt wird.
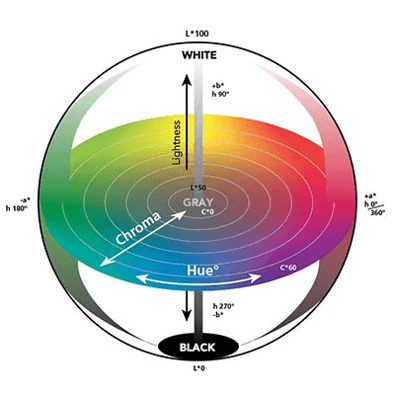
Abb. 6 https://www.xrite.com/blog/tolerancing-part-3
Der Hunter Lab-Farbraum wurde 1966 von R. S. Hunter als visuell homogenerer Farbraum als der CIE 1931 Yxy entwickelt und ist dem CIE Lab Farbraum sehr ähnlich. Er wird heute in vielen Gebieten eingesetzt, darunter auch in der Farbenindustrie in den Vereinigten Staaten, wird aber weniger häufig genutzt als der etwas später entwickelte CIE Lab Farbraum, der mehr Anhänger gefunden hat.
Sowohl die Hunter-Lab- als auch die CIE-Lab-Skala verwenden leicht unterschiedliche Funktionen zur Berechnung der Lab-Werte unter Verwendung der trichromatischen XYZ-Komponenten als Argumente. Hunter Lab führt die Transformation mit Hilfe von Quadratwurzeln durch, während CIE Lab Kubikwurzel-Funktionen verwendet.
Ein weiterer Unterschied ist im Bereich der einzelnen Farbbereiche sichtbar. Die Hunter-Skala schrumpft im gelben Bereich des Farbraums und dehnt sich im blauen Bereich aus. Die CIE-Lab-Skala hingegen dehnt sich im gelben Bereich leicht aus, was deutlicher wird, wenn der CIE-Wert aus der Probe kleiner als eins ist. Ein zusätzlicher Vorteil der CIE-Lab-Skala ist, dass sie in der Regel die visuelle Bewertung von Farbunterschieden bei sehr dunklen Farben besser wiedergibt.
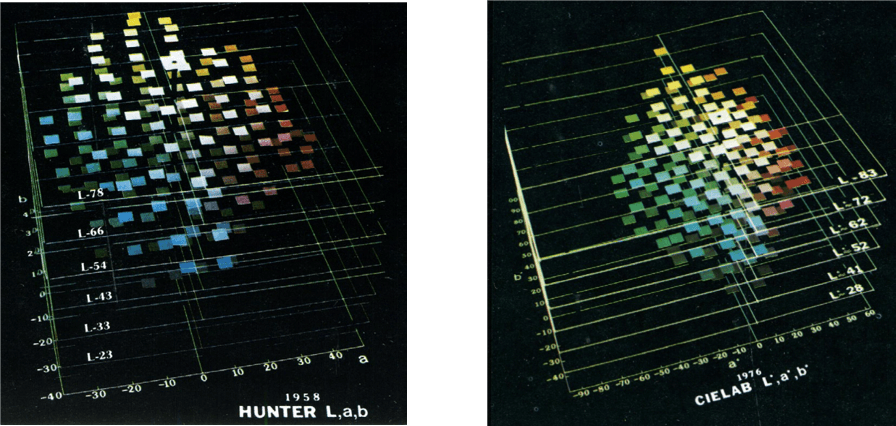
Abb. 7 http://pomiarbarwy.pl/?p=481