Colours have accompanied us since the dawn of time. Every day we can get to know their beauty and diversity anew, because they are still a mystery to us. In our previous articles we talked about what colours are and about colour models depending on devices. This time we would like to introduce you to other models, which were in demand at the beginning of the 20th century.

In 1931, on request of the “Commission Internationale de l’Eclairage” (International Commission on Lighting) there have been developed a colour model independent of devices. It was created on the basis of research carried out on a group of about twenty persons who were able to distinguish colours correctly. This group was shown, in a very narrow field of vision (2o), different colours and had the task of differentiating them. Statistical analysis of the responses allowed to develop a standard observer model. It shows the averaged human capabilities in terms of colour perception (e.g. wavelength range, sensitivity, etc.). Based on the standard observer model, the CIE XYZ model was developed – the first device independent colour model.
The CIE XYZ method is referred to as a colour space which is taken as a reference and standard for other colour spaces created by the “Commission Internationale de l’Eclairage” (CIE LUV, CIE Lab).
The concept of XYZ’s three-chromatic values is based on the idea of seeing colours, which says that the eye is made up of three types of photoreceptors that allow you to see the three basic colours (red, green, blue), while all colours are mixtures of the three basic colours. Therefore, the colour is described in the trichromatic coordinates X,Y,Z. These coordinates correspond to the respective percentages of the three basic colours R (red), G (green), and B (blue).
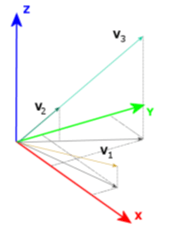
Fig. 1 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
The three-dimensional description of CIE XYZ was transformed into a two-dimensional CIE xyY space. It converts the colour components X, Y, Z to the trichromatic coordinates x, y, Y. The x and y coordinates are responsible for chromaticity and Y for brightness. The xyY space is represented in the colour space, which is the chromaticity graph, as a Maxwell triangle or a colour triangle. This is presented as an area enclosed by two lines – a monochromatic colour curve and a straight purple line.
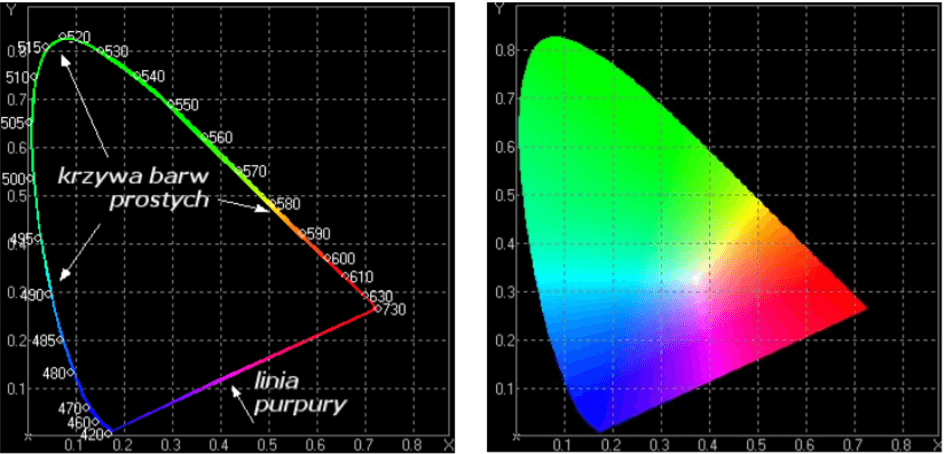
Fig. 2 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
As a result of the work on the issue of perception of colour difference, carried out by Wright, MacAdam and Stiles, the issue of uniformity of colour space was created.
When the CIE XYZ space determines the ranges of colour perception difference (Fig. below), then ellipses of different sizes (so-called MacAdam’s ellipse) will appear. They will be formed in green areas, as ellipses with a relatively large diameter and in blue areas, but here with a relatively small diameter. So when we mark two points in such a space, the human eye can perceive them as two subjectively different hues. On the other hand, two points equally distant in the range of green colours, may determine the colours between which the human eye will not notice the difference, i.e. it will be a subjectively determined one colour.
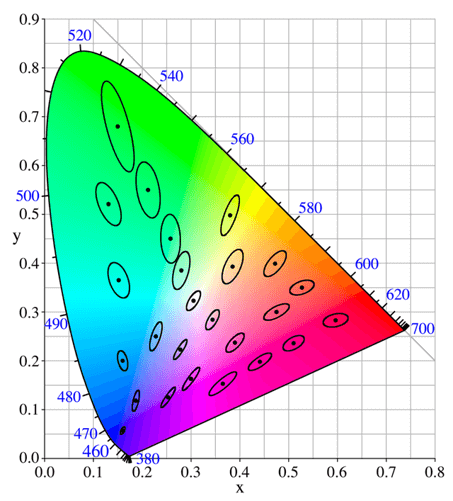
Fig. 3 https://stackoverflow.com/questions/25184748/represent-cie-1931-color-space
Thanks to conducting research on the uniformity of colour space, CIE LUV and CIE Lab were also created.
The CIE LUV model was created (in 1960) as a result of the transformation of xy variables into uv variables. They were supposed to better reflect the differences between colours. During further research, however, it turned out that such a set of variables strongly limits the areas around brown, orange and yellow. The mentioned hues are very important in painting, especially in oil or nature photographs, therefore further attempts at transformation had to be made. In 1976, the u’ and v’ variables were developed, thus creating the CIE LU’V’ space. It is important that the letter “L” in the names comes here from the word “lightness” and just like the “Y” in the xyY model, it defines brightness. Both colour representations obtained are shown in the figure below:
a) CIE uv chart b) CIE u’v’ chart
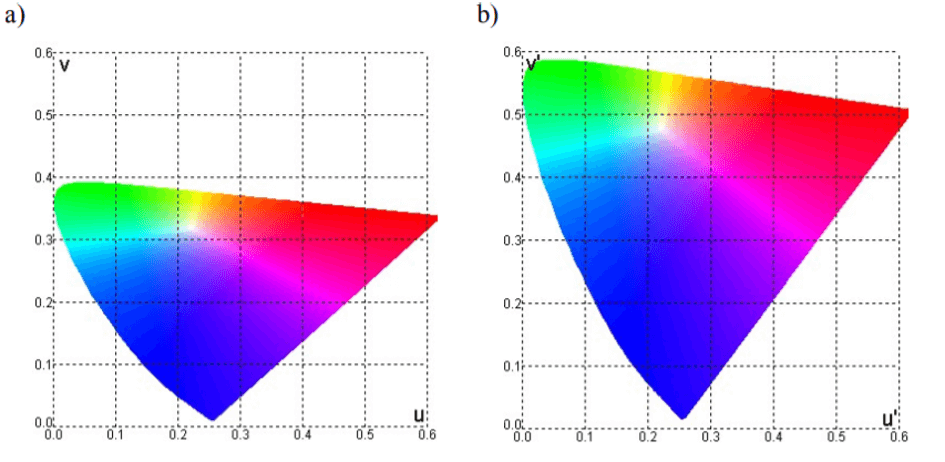
Fig. 4 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf
The second most frequently used colour model independent of the device is the CIE Lab. This is another transformation of CIE XYZ space, which was created in 1976. In defining it, it was assumed that colours which are at the same distance from each other will be perceived as equally different. Assuming that the colour cannot be purple and blue and yellow or green at the same time, the following components have been selected for the description: L – brightness (luminance), a – colour from green to magenta and b – colour from blue to yellow.
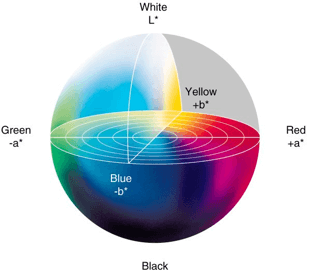
Fig. 5 https://www.researchgate.net/figure/CIE-LAB-1976-color-space_fig2_263697963
However, an important advantage of a given model is the ease of colour comparison. The difference between the two colours in CIE Lab space is expressed as ΔE, which is calculated from the following relationship:
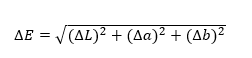
ΔE is the normal Euclidean distance between two points in the three-dimensional space.
It is assumed that a standard observer recognises the colour difference according to the following indicators:0 < ΔE < 1 – sees no difference,
1 < ΔE < 2 – only an experienced observer notices the difference,
2 < ΔE < 3.5 – also an inexperienced observer notices the difference,
3,5 < ΔE < 5 – the observer notices a clear colour difference,
5 < ΔE – the observer perceives the two colours as completely different.
Like the CIE XYZ space, the CIE Lab model is related to the direct perception of colours by the human eye. This is why we refer to it as a device independent colour model.
CIE LCh colour space uses the same scheme as CIE Lab colour space, but uses cylindrical coordinates instead of rectangular ones. In this colour space, L is the brightness and is the same parameter as L in the CIE Lab space, C is the saturation, and h is the hue. The colour saturation value C is 0 in the centre of the sphere, which is the image of the colour space and increases according to the distance from the centre. Shadow h is the angle whose measurement starts at the + a axis and is expressed in degrees.
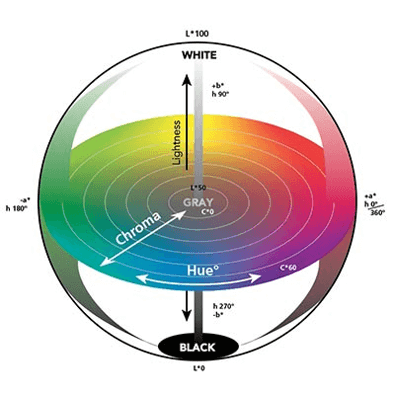
Fig. 6 https://www.xrite.com/blog/tolerancing-part-3
The Hunter Lab colour space was developed in 1966 by R. S. Hunter as a more visually homogenous coluor space than the CIE 1931 Yxy and very similar to the CIE Lab. It is currently in use in various areas, including the paint industry in the United States, however, is applied less often than the CIE Lab space developed a little later, which has gained more supporters.
Both Hunter Lab and CIE Lab scales use slightly different functions to calculate Lab values using XYZ trichromatic components as arguments. Hunter Lab performs the transformation using square roots, while CIE Lab uses cubic root functions.
Another difference is visible in the range of individual colour areas. The Hunter scale shrinks in the yellow area of the colour space and expands in the blue. The CIE Lab scale, on the other hand, is slightly expanded in the yellow area, which is more obvious when the CIE value from the sample is less than one. An additional advantage of the CIE Lab scale is that it usually better reflects the visual assessment of colour differences for very dark colours.
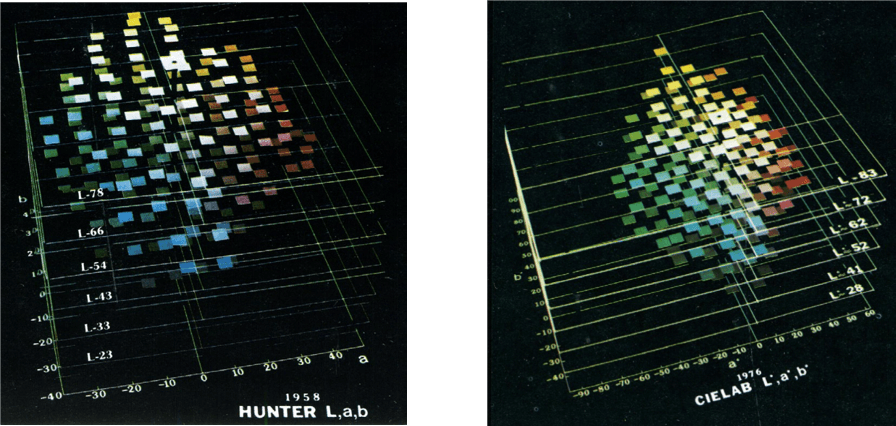
Fig. 7 http://pomiarbarwy.pl/?p=481